AdaMerging: Adaptive Model Merging for Multi-Task Learning
1.文章总结及思考
1.1 背景(动机和挑战)
当前的merge是让多个微调好的模型merge成一个模型后去执行MTL,但这存在几个问题:
- 模型提供者通常只提供微调好的模型,但不提供原始训练数据。
- 多个任务之间会有潜在的冲突以及复杂的相关性。
- 当前基于任务向量的MTL方法比普通的加权平均效果好的多,但和传统的MTL之间仍然存在着明显的差距。
因此挑战点在于如何在不使⽤原始训练数据的情况下更加有效的合并预训练模型,这篇paper提出了AdaMerging来解决这个问题。
1.2 文章工作、横向对比及难点处理
1.2.1 效果总结
效果:这篇paper主要是提出了一种新的自适应、无监督的merge方法–AdaMerging(Task-wise AdaMerging,Task-wise AdaMerging++,Layer-wise AdaMerging, Layer-wise AdaMerging++),由于merge过程中merge系数对模型效果影响较大,本文主要是对如何获取更优效果的merge系数方面做的工作,用熵的最小化作为替代目标来迭代改进模型合并系数,比起现有的普通加权平均、基于任务向量的MTL方法(例如Task Arithmetic和Ties-Merging)在性能、泛化能力、鲁棒性这三个方面都有明显更优的表现。
各方法效果对比:如图所示,该图表示系数$\lambda$对八项任务中各种MTL方法的平均准确率的影响。基于任务向量的Task Arithmetic和Ties-Merging在系数$\lambda=0.3$时达到了最佳的平均准确率,分别为69.1%和72.9%。传统的MTL和AdaMerging分别是88.9%和80.1%,佐证了文章说法。
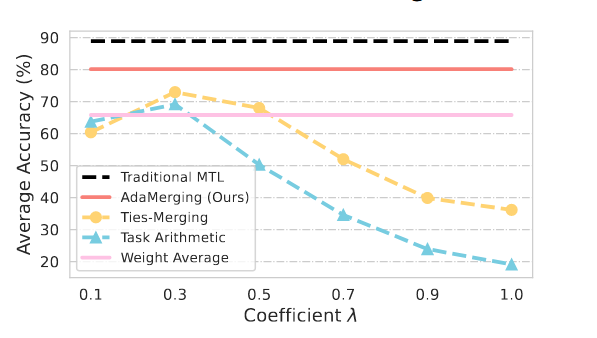
1.2.2 横向对比
基于任务向量的研究忽略了处理各种模型集合时遇到的一个关键挑战,即控制模型合并过程的系数在实现最佳合并性能方面起着关键作用,这篇工作特别强调并解决了这个问题,以弥补性能差距。
这篇工作和现有的基于任务向量的MTL方案的三个区别:
- 以往的在所有任务向量之间共享一个合并系数,限制了任务向量组合的灵活性。AdaMerging在不同的任务甚至不同的层上采用不同的合并系数,大大提高了自适应的灵活性。
- 现有的工作采用网格搜索合并系数,因此缺乏指导原则,在任务数量较大时成本高昂且不可行,这篇工作以熵最小化为替代目标,高效自动地优化合并系数。
- 显著提高了多任务性能、对未知任务的泛化能力以及测试数据分布变化的鲁棒性。
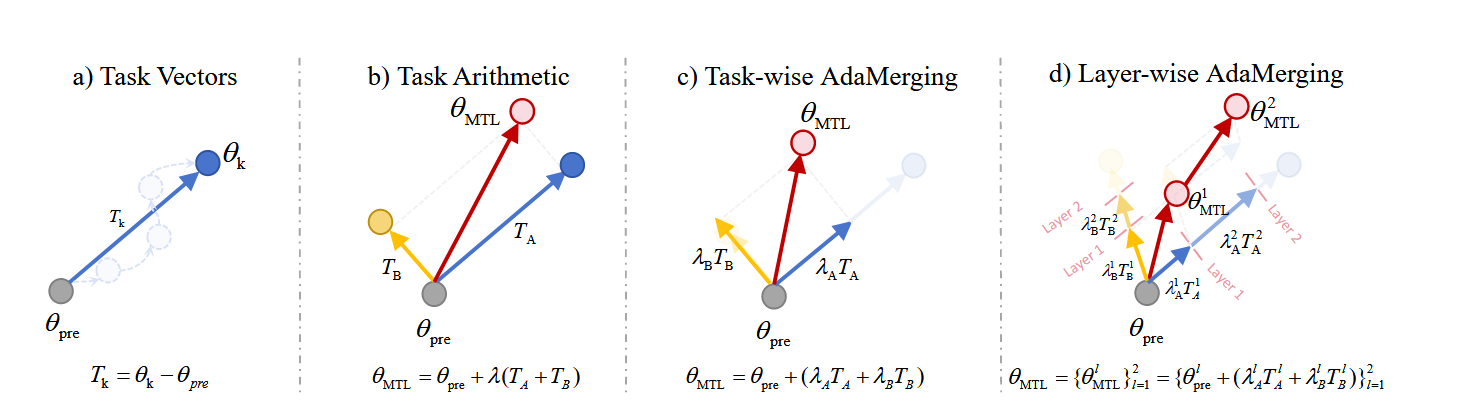
如图所示,图a为任务向量$T_k$的定义,$T_k$是通过在任务$k$的数据上微调好的模型权重$\theta_k$减去预训练权重$\theta_{pre}$获得。图b,对于Task Arithmetic,它将多个任务向量添加到预训练的权重$\theta_{pre}$中以执行MTL。在此基础上,图c中Ties-Merging表明一些任务向量的参数值可能是冗余的,或者参数符号可能存在冲突,直接合并会导致性能损失,因此它会去除一些冗余参数,使其不加入计算。Task Arithmetic和Ties-Merging都比简单的加权平均效果好得多,但和传统的MTL之间仍然存在着明显的差距。这篇文章认为基于任务向量的模型合并方法对合并系数$\lambda$非常敏感。不合适的$\lambda$将导致性能低于加权平均值,甚至达到不可接受的低精度。当任务数量较大时,网格搜索每个任务向量的合并系数代价高昂。因此他在合并系数这方面进行了细分,对不同的任务或是不同任务的不同层都会产生各自的merge系数。
1.2.3 难点处理
1.2.3.1 模型merge过程对merge系数敏感
对于任务之间的潜在冲突以及复杂的相关性,这篇工作采用任务向量的方法去尽可能减少任务之间的冲突,保持任务之间的独立。但由于模型merge对merge系数非常敏感,因此这篇文章针对不同任务甚至不同层都进行了merge系数的细分。
Task-wise AdaMerging:如1.2.2图所示,Task-wise AdaMerging给每个任务向量$T_k$都分配了一个独立的合并系数$\lambda_k$,也就是:$\theta_{MTL}=\theta_{pre}+\sum_{k=1}^K\lambda_kT_k$. Task-wise AdaMerging允许对平均MTL性能有正向传导的任务向量$T_k$在$\theta_{MTL}$中占据更大的份额,而对MTL有害的任务向量$T_{k\prime}$则减少他对合并权重$\theta_{MTL}$的贡献,因此可以提高平均MTL性能。
Layer-wise AdaMerging:Task-wise AdaMerging可能不足以减轻任务向量的干扰。在深度神经网络模型中,每一层学到的信息都是不同的。。因此,在合并任务向量的时候,每个任务向量$T_k$的不同层的权重$\{T_k^1,T_k^2,...,T_k^L\}$也应该对最终的多任务权重$\theta_{MTL}$有不同的贡献$\{\lambda_k^1,\lambda_k^2,...,\lambda_k^L\}$。因此得到了:$\theta_{MTL} = \{\theta_{MTL}^l\}_{l=1}^L = \{\theta_{pre}^l + \sum_{k=1}^K\lambda_k^lT_k^l\}_{l=1}^L$,其中$L$代表层的数量。
这篇文章在此基础上参考了Task Arithmetic和Ties-Merging的思想,认为他的这种方法也会有冗余值和符号冲突的问题,借鉴了Ties-Merging的处理方法得到了AdaMerging的变体,AdaMerging++,即在AdaMerging的基础上删除冗余值和符号冲突。相应的有Task-wise AdaMerging++和Layer-wise AdaMerging++,分别可以形式化为:$\theta_{MTL}=\theta_{pre}+\sum_{k=1}^K\lambda_k\Phi(T_k)$和$\theta_{MTL}=\{\theta_{pre}^l\}_{l=1}^L=\{\theta_{pre}^l + \sum_{k=1}^K\lambda_k^l\Phi(T_k^l)\}_{l=1}^L$.
1.2.3.2 只有任务向量但是没有初始训练数据
这篇工作解决这个问题用了test-time adaption,在看不见的测试数据上调整训练模型的权重,以应对测试数据上的分布变化。
1.3 实验
在8个图像分类数据集上做了基于任务向量的多任务模型合并实验,实验基线主要分成两类,一类是非模型合并–个人的和传统的MTL,另一类是各种先进的模型合并方法,包括平均加权,Fisher Merging,Regmean,Task Arithmetic和Ties-Merging。具体数据对比见论文表格。
2.知识点基础
2.1 Multi-Task Learning:什么是多任务学习?
一种机器学习的方法,旨在同时学习多个相关任务,以提高模型在这些任务上的性能,核心思想是利用任务之间的相关性,共享模型参数,从而提高模型的学习效果和泛化能力。
优点:
1.提高泛化能力:通过同时学习多个任务,模型可以学习到更为通用的特征表示,从而提高在新任务上的泛化能力。
2.减少过拟合:多任务学习可以增加模型的正则化效果,减少过拟合风险。
3.提高学习效率:通过共享参数,模型可以更高效地利用数据,减少训练数据和计算资源。
挑战:
1.任务相关性:任务之间需要有一定的相关性,否则共享参数无法有效提高性能。
2.任务冲突:不同任务对模型参数可能会有不同的需求,导致任务之间的冲突。
3.平衡任务权重:需要合理分配每个任务的权重,以确保模型在所有任务上都能取得良好的性能。
2.2 grid search:传统的网格搜索是怎么做的?
一种调参手段;穷举搜索,在手动列出的所有候选的参数选择中,通过循环遍历,尝试每一种可能性,表现最好的参数就是最终的结果。(就是暴力搜)
2.3 combinatorial optimization search: 什么是组合优化搜索?
组合优化问题,Combinatorial Optimization Problem,简称COP,是一类在离散状态下求极值的最优化问题,组合优化搜索是在有限的解空间中寻找目标函数最优解的搜索方法。<font color="red">网上帖子基本都是关于组合优化问题的定义和分类解释,关于这种搜索方式只提到是在有限解空间中进行的搜索最优解,具体怎么实现没找到,需要找人问下 </font>
2.4 Spearman correlation coefficient:斯皮尔曼相关系数是什么?
相关系数是对两个变量的相对运动之间关系强度的统计量度。值范围在 -1.0 和 1.0 之间。-1.0 的相关性表示完全的负相关,而 1.0 的相关性表示完全的正相关。0.0 的相关性表明两个变量的移动之间没有线性关系。
Pearson Correlation Coefficient(皮尔逊相关系数)是衡量两个变量$X$和$Y$之间线性相关性的统计量。他的值介于+1和-1之间。+1 完全正线性相关,0 是无线性相关,-1 是完全负线性相关。皮尔逊相关性只能评估两个连续变量之间的线性相关(仅当一个变量的变化与另一个变量的比例变化相关时,关系才是线性的)
Spearman correlation coefficient是排序相关性(ranked values)的非参数度量,使用单调函数描述两个变量之间的关系的程度。Spearman相关性可以评估两个变量之间的单调关系一一有序,它基于每个变量的排名值(ranked value)而不是原始数据(original value)。如 orginal value(1,3,5,8,20,30,…) => ranked value (1,2,3,4,5,6…)
总结,Pearson相当于捕获线性关系,Spearman相当于捕获单调性或一种上升下降的趋势。
2.5 Task Arithmetic:什么是任务算法?
Task Arithmetic是一种用于合并和编辑预训练模型的方法,通过简单的算术操作(如加法、减法和取反)来调整模型的行为。这种方法的核心思想是利用任务向量(Task Vectors)来表示从预训练模型到特定任务微调后模型的权重变化。<font color="red">Task Arithmetic论文待看,计划5.19-5.30两周内看完 </font>[2212.04089] Editing Models with Task Arithmetic
2.6 Ties-Merging: 什么是领带合并?
Ties-Merging是一种用于合并多个特定任务模型的方法,旨在减少模型融合过程中的干扰,从而提高融合模型的性能。该方法的核心思想是通过三个步骤(Trim、Elect、Disjoint Merge)来解决冗余参数带来的干扰和参数符号不一致的干扰。
2.7 什么是Fisher Merging?Fisher information matrix?
Fisher信息矩阵$F_\theta$是一个衡量模型参数重要性的矩阵,反映了每个参数对模型输出的影响程度。Fisher信息矩阵的对角线元素表示每个参数的重要性。Fisher Merging是一种基于Fisher Information Matrix的模型合并技术,旨在通过加权平均的方式合并多个模型的参数,以提高合并后模型的性能。相关论文见[2111.09832] Merging Models with Fisher-Weighted Averaging,<font color="blue">重要不紧急,打算看 </font>
2.8 模型之间的L2距离是指什么?
模型之间的L2距离(欧氏距离)是一种衡量两个模型参数差异的方法,提供了一个量化的方式来评估两个模型参数之间的相似性或差异性。公式:
$$ L2\ Distance={\sqrt{\sum\limits_{i=1}^n(\theta_{1,i}-\theta_{2,i})^2}} $$其中$n$为参数向量的长度。
L1距离(曼哈顿距离)是一种衡量两个向量之间差异的方法,提供了一种量化的方式来评估两个向量(例如模型参数、特征向量等)之间的相似性或差异性。公式:
$$ L1\ Distance=\sum\limits_{i=1}^n|a_i-b_i| $$其中$n$是向量的长度,$a_i$和$b_i$分别是两个向量中的第$i$个元素。
2.9 什么是PEM Composition?
Composing Parameter-Efficient Modules with Arithmetic Operations(PEM)方法旨在通过简单的算术操作(如加法、减法和取反)来组合参数高效的模块,从而实现高效的模型融合和编辑。这种方法的核心思想是利用任务向量(Task Vectors)来表示从预训练模型到特定任务微调后模型的权重变化,并通过算术操作来组合这些任务向量,以生成新的模型参数。
对应应该是这篇工作:[2306.14870] Composing Parameter-Efficient Modules with Arithmetic Operations
2.10 test data distribution shifts是什么?
测试数据分布变化(Test Data Distribution Shift)是指在机器学习模型的测试阶段,测试数据的分布与训练数据的分布不一致的情况。这种分布变化可能会导致模型性能下降,因为它在训练时学习到的模式可能不再适用于新的测试数据。变化原因可能是因为训练数据和测试数据数据收集时间不同、数据来源不同、数据预处理不同或是测试环境可能和训练环境不同等。
2.11 ViT和BERT?
ViT是一种基于 Transformer 架构的计算机视觉模型,通过将图像分割成 Patch 并使用自注意力机制捕捉长距离依赖关系,适用于图像分类、目标检测和语义分割等任务。
BERT是一种基于 Transformer 架构的自然语言处理模型,通过 Masked Language Model 和 Next Sentence Prediction 任务进行预训练,适用于文本分类、问答、命名实体识别等任务。
2.12 test-time adaption?
传统的模型训练后固定,在测试时无法改变。TTA是一种在模型部署后,利用少量未标记的测试数据来微调模型的技术。这种方法旨在提高模型在新环境或新任务中的适应性和性能,而无需重新训练整个模型。
实现方法:
1.伪标签生成:使用模型的预测结果为未标记的测试数据生成伪标签。这些伪标签可以用于微调模型。
2.微调模型:使用生成的伪标签和少量未标记的测试数据来微调模型。微调过程通常只涉及模型的部分参数,以减少计算成本。
3.迭代优化。
2.13 Shannon entropy?
香农熵用于量化信息的不确定性或信息量,是衡量信息源或随机变量不确定性的度量。
定义:对于一个离散随机变量$X$,其可能取值为$\{x_1,x_2,...,x_n\}$,对应概率分别为$P(x_1),P(x_2),...,P(x_n)$,香农熵$H(X)$定义为:
$$ H(X)=-\sum\limits_{i=1}^nP(x_i)logP(x_i) $$其中,对数通常以2为底,此时熵的单位是bit。如果以 e 为底,单位是nat。
2.14 Motion Blur,Impulse Noise,Gaussian Noise,Pixelate,Spatter,Contrast and JPEG Compression分别是什么类型的污染?
Motion Blur(运动模糊)是由于相机或拍摄对象在拍摄过程中移动而产生的模糊效果。这种模糊通常是沿着运动方向的。运动模糊会降低图像的清晰度,使得边缘检测和特征提取变得更加困难。
Impulse Noise(脉冲噪声)是一种随机出现的噪声,通常表现为图像中的一些像素值突然跳变到极值(如最大值或最小值)。这种噪声通常是由传感器故障或传输错误引起的。脉冲噪声会干扰图像的像素值,使得图像处理算法(如滤波和边缘检测)的性能下降。
Gaussian Noise(高斯噪声)是一种统计噪声,其概率密度函数符合正态分布(高斯分布)。这种噪声通常是由传感器的热噪声或电子元件的随机波动引起的。高斯噪声会增加图像的噪声水平,使得图像处理算法(如平滑和特征提取)的性能下降。
Pixelate(像素化)是将图像分割成较大的像素块,每个块内的像素值被设置为该块的平均值。这种效果通常用于降低图像的分辨率或保护隐私。像素化会降低图像的分辨率,使得图像处理算法(如超分辨率和特征提取)的性能下降。
Spatter(飞溅)是一种模拟液体飞溅效果的干扰,通常用于图像增强或艺术效果。飞溅效果会干扰图像的背景和前景,使得图像分割和目标检测变得更加困难。
Contrast(对比度)是指图像中明暗区域的差异。降低对比度会使图像的明暗差异减小,而增加对比度会使明暗差异增大。对比度调整会影响图像的视觉效果和处理算法的性能,如直方图均衡化和特征提取。
JPEG Compression(JPEG 压缩)是一种有损压缩算法,通过减少图像中的冗余信息来减小文件大小。压缩过程中会引入一些失真。JPEG 压缩会降低图像的质量,使得图像处理算法(如边缘检测和特征提取)的性能下降。
