多臂老虎机(MAB)
多臂老虎机可以看作是一个简易版的强化学习问题,其中不存在状态,只有动作与奖励。
问题定义
在一个 $ K $ 根拉杆的多臂老虎机中,每个拉杆都对应于一个奖励的概率分布 $ \R $ ,拉下拉杆就能从该拉杆的对应的奖励概率分布中获得一个奖励 $ r $ 。在每个拉杆的奖励概率分布未知的情况下,从头开始尝试,目标是在 $ T $ 次拉杆后获得尽可能高的累积奖励。
由于奖励的概率分布是未知的,因此需要在“探索拉杆的获奖概率”以及“根据经验选择获奖最多的拉杆”之间探索,即 探索与利用 问题。
形式化描述
多臂老虎机问题可以表示为一个元组 $ \langle \mathcal{A},\mathcal{R} \rangle $ ,其中:
- $ \mathcal{A} $ 为动作集合,其中一个动作表示拉动一个拉杆。若多臂老虎机有 $ K $ 根拉杆,那么动作空间的集合为 $ \{ a_1,...,a_k \} $ ,我们用 $ a_t \in \mathcal{A} $ 表示任意一个动作
- $ \mathcal{R} $ 为奖励概率分布,拉动每一根拉杆的动作 $ a $ 都对应一个奖励概率分布 $ \mathcal{R(r|a)} $ ,不同拉杆的奖励分布通常不同
假设每个时间只能拉动一个拉杆,多臂老虎机的目标为最大化一段时间步 $ T $ 内累积的奖励: $ max \sum_{t=1}^T r_t, r_t ~ \mathcal{R(\cdot|a_t)} $
累积懊悔
对于每个动作,定义其期望奖励为 $ Q(a) = \mathbb{E}_{r \sim R(\cdot|a)}[r] $ 。因为至少存在一个拉杆其期望奖励大于其他任意一根拉杆,我们将其表示为 $ Q^* = max_{a \in \mathcal{A}}~Q(a) $ 。为了更加直观的观察拉动一根拉杆与最优奖励的差距,引入 懊悔(regret) 概念,即 $ R(a) = Q^* - Q(a) $ 。累积懊悔 即操作T次后的懊悔总量,即 $ \sigma_R=\sum_{t=1}^TR(a_t) $ ,因此MAB问题的目标为最大化奖励,同时等价于最小化累积懊悔。
估计期望奖励
为了知道拉动拉杆所能得到的奖励,我们需要估计拉杆的期望奖励,由于拉动一次的奖励存在随机性,因此需要多次拉动计算期望,其算法流程如下:
for a in A:
N(a) = 0 # 初始化 计数器
Q(a) = 0 # 初始化 期望奖励
for t in range(1, T + 1):
a_t = select()
r_t = get_value(a_t)
N(a_t) = N(a_t) + 1
Q(a_t) = Q(a_t) + [r_t - Q(a_t)] / N(a_t)
上述内容推导如下: $ $ Q_k = \frac{1}{k} \sum_{i=1}^k r_i \ =\frac{1}{k}(r_k + \sum_{i=1}^{k-1} ri) \ =\frac{1}{k}(r_k + (k-1)Q_{k-1}) \ =\frac{1}{k}(r_k + kQ_{k-1} - Q_{k-1}) \ =Q_{k-1} + \frac{(r_k - Q_{k-1})}{k} $ $
采用上述方式更新每次的时间复杂度和空间复杂度都为 O(1)
探索与利用
多臂老虎机问题即如何平衡探索与利用的次数达到最大的总奖励或最小的懊悔值。
贪心算法
$ \epsilon $ -贪心算法
最简单的方式是直接选择贪心算法,即一直选择获得最大奖励的拉杆进行拉动,但多臂老虎机的奖励分布未知,因此对其进行修改,形式如下: $ $ a_t = \begin{cases} argmax_{a\in\mathcal{A}} ~ \hat Q(a) ~~采样概率:1 - \epsilon \ random_sample(\mathcal{A}) ~~采样概率:\epsilon \end{cases} $ $
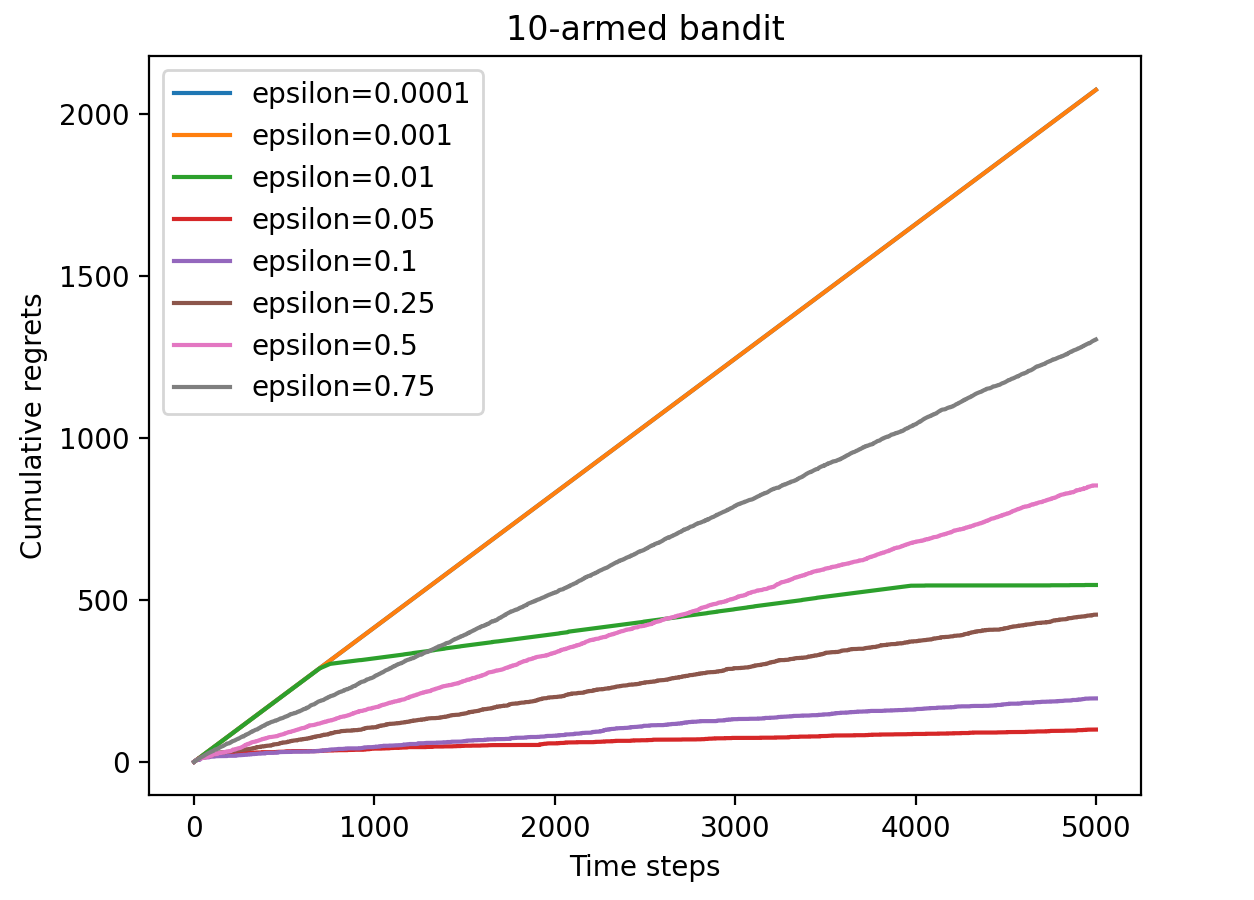
可以看到无论 $ \epsilon $ 取值为多少,懊悔之都呈现近乎线性的增长曲线,这是由于只要做出了随机拉杆选择的选项那么此时就一定会产生期望固定的懊悔值
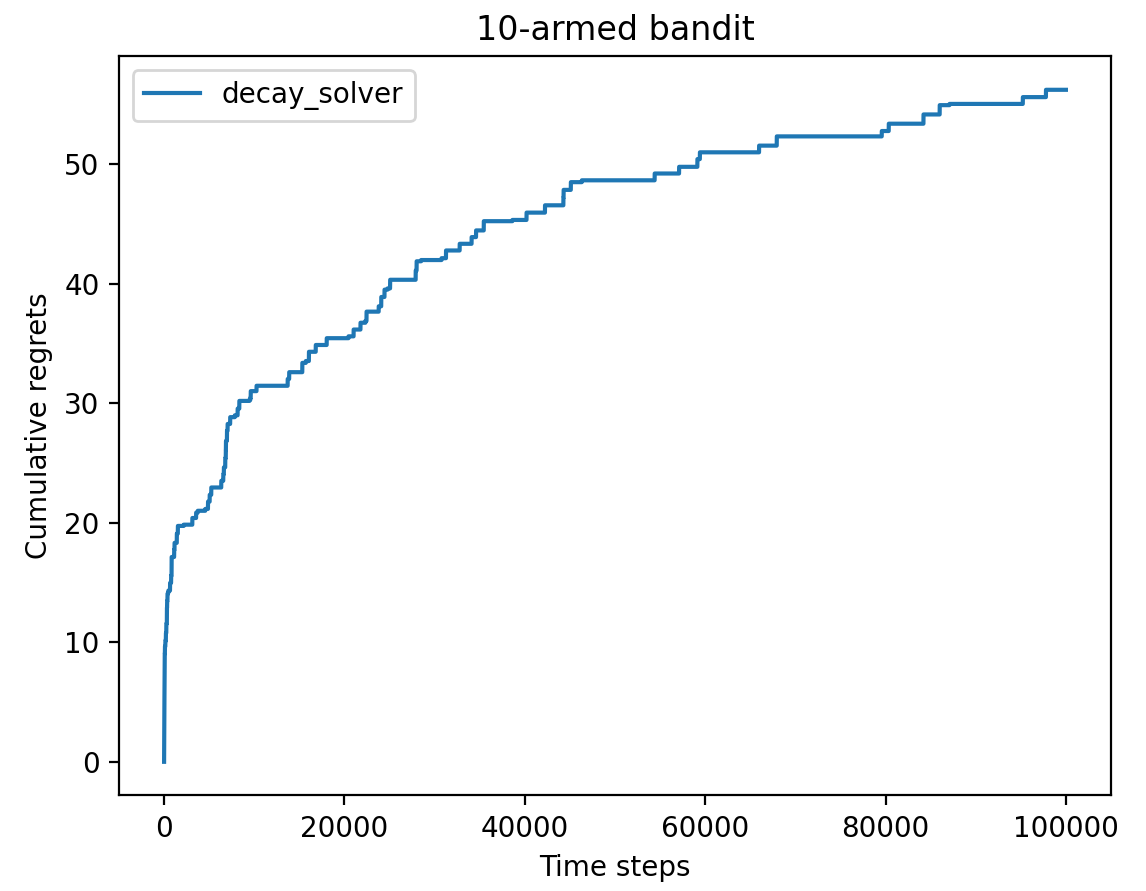
时间衰减的 $ \epsilon $ -贪心算法
我们对 $ \epsilon $ 进行衰减处理,采用反比例衰减,即 $ \epsilon_t=\frac{1}{t} $ ,开始时探索概率更高,后续逐渐衰减为利用概率更高。可以看到采用衰减的 $ \epsilon $ 得到的懊悔增长先快后慢
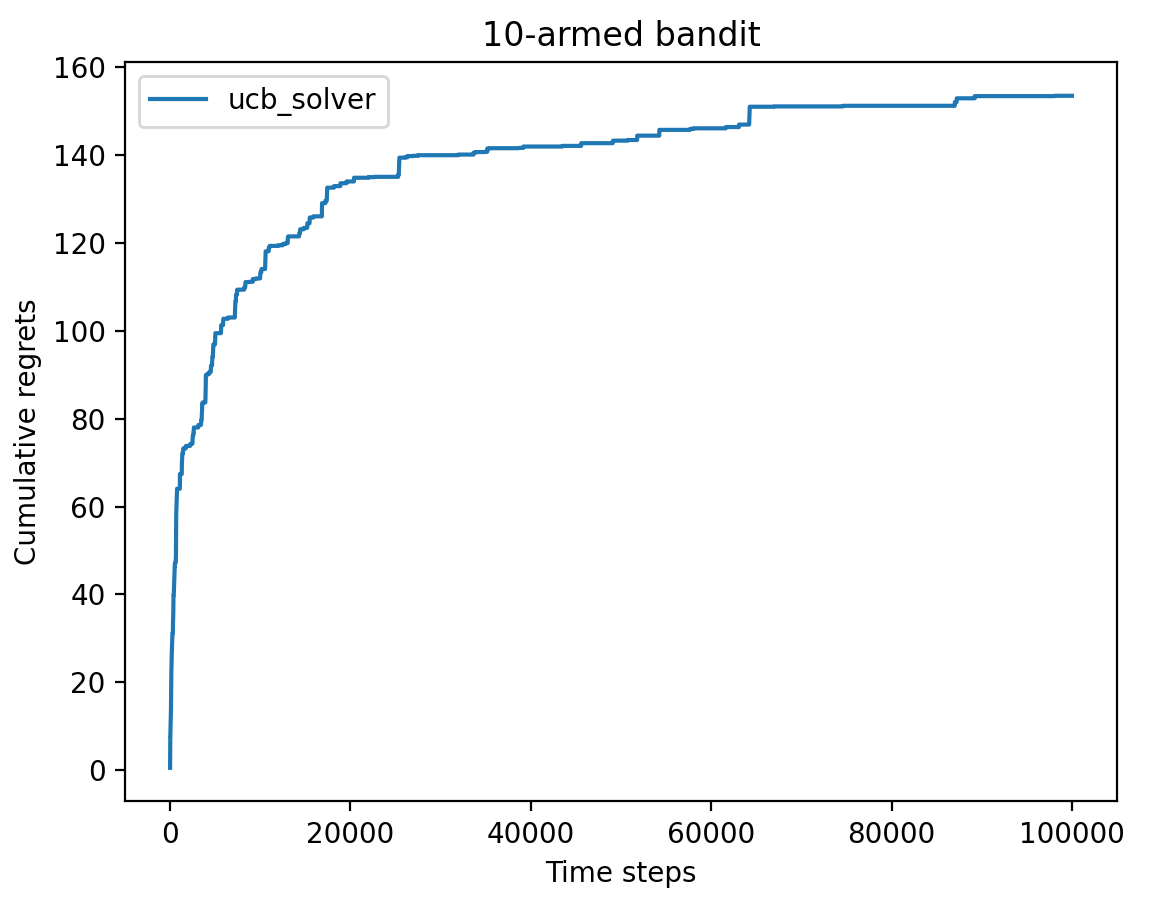
上置信界算法
假设一种情况,一个两臂老虎机,其中第一个杠杆只拉动了一次,奖励为0,另一个杠杆拉动了很多次,基本摸清了他的奖励分布,这时会有两种选择?有可能是进一步尝试第一个杠杆,去进一步确定这个杠杆的奖励分布,也有可能会直接采用第二根杠杆得到大致确定的奖励。这是由于 不确定性 导致,对于第一个杠杆不确定性很高,而第二个杠杆很低。 这是由于第一个杠杆具有很大的探索价值,有可能经过探索发现其期望奖励非常大。因此引入不确定性度量 $ U(\alpha) $ ,它会随着使用次数增加和减小,然后就可以基于不确定性的策略来综合考虑现有的期望奖励估值和不确定性,其核心问题就是如何估计不确定性。
上置信界(upper confidence bound, UCB) 算法是一种经典的基于有不确定性的策略算法。
假设一个按钮的真实奖励概率为 $ p $ ,我们拉动了 $ n $ 次,其中 $ n_r $ 次获得了奖励,那么我们的预估奖励概率为 $ \widetilde{p} $ 。如果能根据经验找到一个 $ \delta $ ,使得 $ p \le \widetilde{p} + \delta $ 恒成立,那么就可以认为 $ \widetilde{p} + \delta $ 是 $ p $ 的上界。因此在 $ \widetilde{p} $ 确定的情况下, $ \delta $ 决定了 $ p $ 的范围,即 $ \delta $ 可以一定程度的反映按钮此时的不确定性。
如何找到 $ \delta $
此处引入 霍夫丁不等式(Hoeffding’s inequality)
【霍夫丁不等式】设 $ X_1, ..., X_n $ 为 $ n $ 个取值为 $ [0,1] $ 之间的独立同分布的变量,用 $ \widetilde{p} = \frac{1}{n} \sum_{j=1}^n X_i $ 表示其样本均值,用 $ p $ 表示实际均值,那么有 $ P\{p-\widetilde{p} \le \delta \} \ge 1 - e^{-2n \delta^2} $
经过变换可以得到 $ P\{p \le \widetilde{p} + \delta \} \ge 1 - e^{-2n \delta^2} $
此时经过拉动杠杆我们得到了样本均值 $ \widetilde{p} $ ,想要让 $ p \le \widetilde{p} + \delta $ 恒成立这是不现实的,因此在容忍一些小差错的前提下,使得其尽可能接近100%,即让 $ 1 - e^{-2n\delta^2} $ 尽可能大,这样 $ P\{p \le \widetilde{p} + \delta \} $ 就会尽可能的大
因此需要找到一个表示方法,让 $ 1 - e^{-2n\delta^2} $ 尽可能接近于1。思考对于总共拉动 $ N $ 次拉杆(所有拉杆的次数之和)可以得到的最大的预估奖励是多少?由于要找到不等于1但无限接近于1的方案,因此可以得到的最大预估奖励为 $ \frac{N-1}{N} $
此时令 $ 1-e^{-2n\delta^2} = \frac{N-1}{N} $ ,通过变换可以得到 $ \delta = \sqrt{\frac{\ln{N}}{2n}} $ ,即在 $ \delta $ 满足左侧等式的情况下, $ p \le \widetilde{p} + \delta $ 几乎恒成立
基于 $ \delta $ 如何进行按钮选择
通过上述内容得到 $ \delta = \sqrt{\frac{\ln{N}}{2n}} $ ,但其中 $ \frac{N-1}{N} $ 是拍脑袋想的,还需要进一步分析是否合适
- 当 $ n $ 不变,$N$增大,即我们选择按其他按钮,而这个按钮不变,此时 $\delta$ 即不确定性(相对于其他按钮)增大
- 当 $ N $ 不变,$n$增加,即按当前按钮的比例增大,此时该按钮不确定性(相对于其他按钮)降低
由于上述分析,可以认为$\delta$合理
此时对于每个按钮来说其能得到的预估奖励为 $ \widetilde{p} + \delta = \frac{n_r}{n} + \sqrt{\frac{\ln{N}}{2n}} $,每次都去选择预估奖励最大的拉杆进行拉动
实际使用时为了防止出现分母为 $ 0 $ 的情况,对分母都进行 $ +1 $操作 ,此外为了调节利用与探索,使用时会在不确定性前加入超参数 $ c $ 以调节不确定性的影响,最终使用的奖励估计如下:
$$ UCB = \frac{n_r}{n + 1} + c * \sqrt{\frac{\ln{N}}{2n + 1}} $$可以看出 $ UCB $ 算法得到的结果也是通过少量探索次数后,懊悔值上升就非常缓慢了
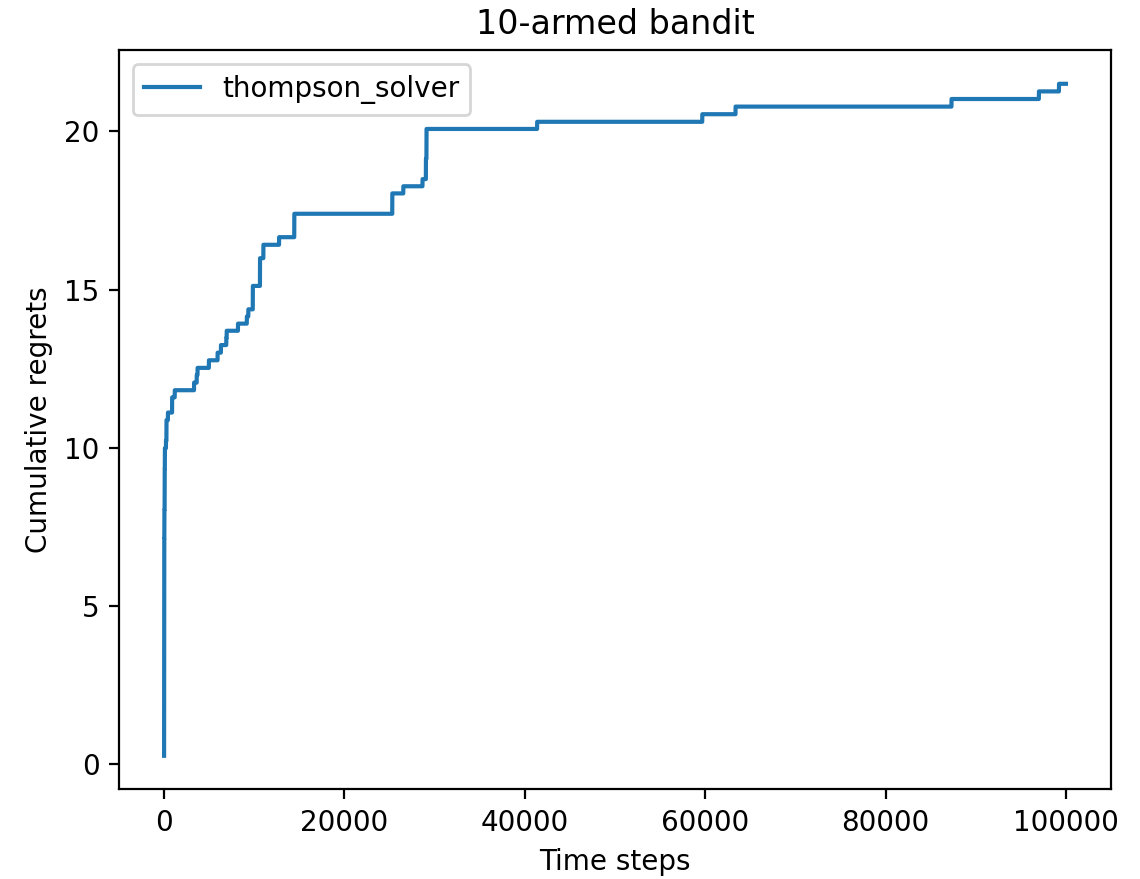
汤普森采样算法
假设奖励服从一个期望分布,每次只需要从期望奖励中进行算则即可,但计算所有拉杆的期望奖励代价较高。因此汤普森采样算法是通过采样的方式,对每个动作 $ a $ 的奖励概率分布进行一次采样,得到一组每个拉杆一个的奖励样本,再从中选取最大的奖励动作。
对于 $ [0, 1] $ 这种二分类奖励,直接将其看作服从 $ (a, b) $ 的 $ Beta $ 分布。那么对于每个拉杆,当选中其拉动得到奖励,则将分布变为 $ (a + 1, b) $ ,否则将其变为 $ (a, b + 1) $ 的分布。